时间复杂度,空间复杂度和稳定性
时间复杂度
指的是算法执行语句的次数(取最多次数的那个语句来表示)
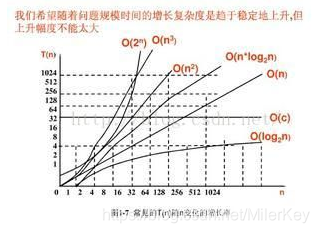
a^x^ =N(a>0,且a≠1) ==> x=logaN
注: Hash的查找的时间复杂度是1,原因“key-value键值对”,离散的
下面是3个例子关于while简单的理解一下时间复杂度
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
| //第一个算法执行次数是20,常量所以是O(1)
int x = 1;
while (x<20)
{
x++;
}
//第二个执行次数是n决定,O(n)
int x = 1;
while (x<n)
{
x++;
}
// 执行次数由 c 和 n共同决定,c = 1 时,O(1),c != 1时,O(n)
int x = 1;
c = c or 1;
while (x<n && c != 1)
{
x++;
}
|
再来看一个简单插入排序
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
| #include <stdio.h>
// 分类 ------------- 内部比较排序
// 数据结构 ---------- 数组
// 最差时间复杂度 ---- 最坏情况为输入序列是降序排列的,此时时间复杂度O(n^2)
// 最优时间复杂度 ---- 最好情况为输入序列是升序排列的,此时时间复杂度O(n)
// 平均时间复杂度 ---- O(n^2)
// 所需辅助空间 ------ O(1)
// 稳定性 ------------ 稳定
int main()
{
int A[] = { 6, 5, 3, 1, 8, 7, 2, 4 };// 从小到大插入排序
int n = sizeof(A) / sizeof(int);
int i, j, get;
for (i = 1; i < n; i++) // 类似抓扑克牌排序
{
get = A[i]; // 右手抓到一张扑克牌
j = i - 1; // 拿在左手上的牌总是排序好的
while (j >= 0 && A[j] > get) // 将抓到的牌与手牌从右向左进行比较
{
A[j + 1] = A[j]; // 如果该手牌比抓到的牌大,就将其右移
j--;
}
A[j + 1] = get;// 直到该手牌比抓到的牌小(或二者相等),将抓到的牌插入到该手牌右边(相等元素的相对次序未变,所以插入排序是稳定的)
}
printf("插入排序结果:");
for (i = 0; i < n; i++)
{
printf("%d ", A[i]);
}
printf("\n");
return 0;
}
|
改进一下,第二层采用二分查找法
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
| #include <stdio.h>
// 分类 -------------- 内部比较排序
// 数据结构 ---------- 数组
// 最差时间复杂度 ---- O(n^2)
// 最优时间复杂度 ---- O(nlogn)
// 平均时间复杂度 ---- O(n^2)
// 所需辅助空间 ------ O(1)
// 稳定性 ------------ 稳定
int main()
{
int A[] = { 5, 2, 9, 4, 7, 6, 1, 3, 8 };// 从小到大二分插入排序
int n = sizeof(A) / sizeof(int);
int i, j, get, left, right, middle;
for (i = 1; i < n; i++) // 类似抓扑克牌排序
{
get = A[i]; // 右手抓到一张扑克牌
left = 0; // 拿在左手上的牌总是排序好的,所以可以用二分法
right = i - 1; // 手牌左右边界进行初始化
while (left <= right) // 采用二分法定位新牌的位置
{
middle = (left + right) / 2;
if (A[middle] > get)
right = middle - 1;
else
left = middle + 1;
}
for (j = i - 1; j >= left; j--) // 将欲插入新牌位置右边的牌整体向右移动一个单位
{
A[j + 1] = A[j];
}
A[left] = get; // 将抓到的牌插入手牌
}
printf("二分插入排序结果:");
for (i = 0; i < n; i++)
{
printf("%d ", A[i]);
}
printf("\n");
return 0;
}
|
再改进一下,成为希尔排序
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
| #include <stdio.h>
// 分类 -------------- 内部比较排序
// 数据结构 ---------- 数组
// 最差时间复杂度 ---- 根据步长序列的不同而不同。已知最好的为O(n(logn)^2)
// 最优时间复杂度 ---- O(n)
// 平均时间复杂度 ---- 根据步长序列的不同而不同。
// 所需辅助空间 ------ O(1)
// 稳定性 ------------ 不稳定
int main()
{
int A[] = { 5, 2, 9, 4, 7, 6, 1, 3, 8 };// 从小到大希尔排序
int n = sizeof(A) / sizeof(int);
int i, j, get;
int h = 0;
while (h <= n) // 生成初始增量
{
h = 3*h + 1;
}
while (h >= 1)
{
for (i = h; i < n; i++)
{
j = i - h;
get = A[i];
while ((j >= 0) && (A[j] > get))
{
A[j + h] = A[j];
j = j - h;
}
A[j + h] = get;
}
h = (h - 1) / 3; // 递减增量
}
printf("希尔排序结果:");
for (i = 0; i < n; i++)
{
printf("%d ", A[i]);
}
printf("\n");
return 0;
}
|
空间复杂度
指对一个算法在运行过程中临时占用存储空间,看你开辟的临时空间就好了。
稳定性
排序稳定性
指的是针对相同数值,在排序前后是否有发生变化的可能。一般举返例来证明
这只是一个例子来说明稳定性,大家普遍说冒泡是稳定的,条件换成“>=”导致算法不稳定,建议不要
下面是个简单冒泡排序来排序{1,1,1,1,1,1,2, 2,1}
1
2
3
4
5
6
7
8
9
10
| for (int j = 0; j < n - 1; j++)
{
for (int i = 0; i < n - 1 - j; i++)
{
if (A[i] > A[i + 1]) // 如果条件改成A[i] >= A[i + 1],则变为不稳定的排序算法
{
exchange(A, i, i + 1);
}
}
}
|
数值稳定性
讨论的是计算机编程中,由于四舍五入等导致的结果偏差。
- 尽量减少运算次数
- 加法运算时,避免大数加小数
- 避免两个相近的数相减
- 避免小数做除法或者大数做乘法
附录
常见排序总结
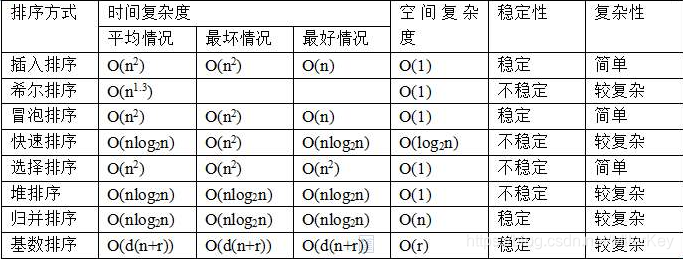
编程排序算法

